赌徒破产问题中押注次数的数学期望求解

有一天我的朋友发了这样一个图，问要怎么求解：

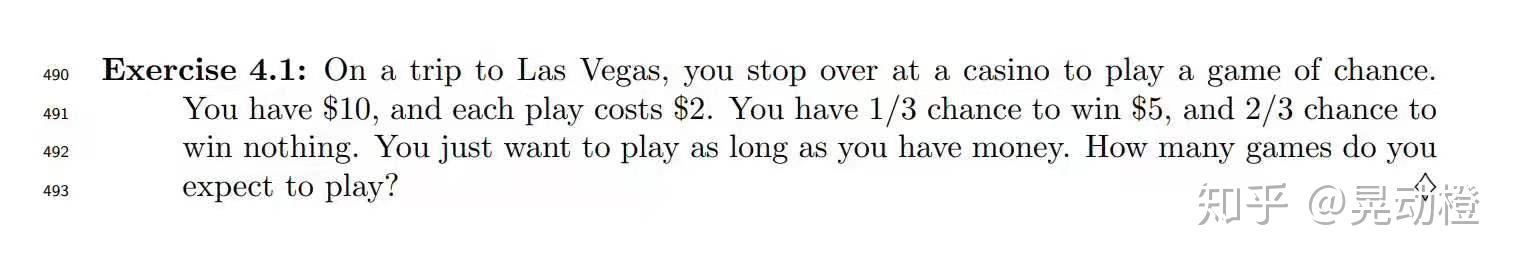
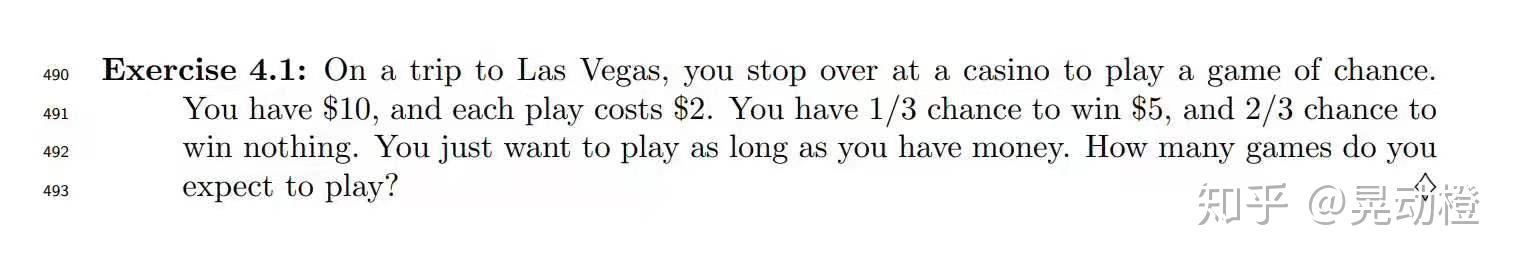
这是个【赌徒破产问题】，我一开始以为可以求得到解析解，历尽周折，无功而返，我眉头一皱，发现问题并不简单，于是找了很多资料，最后形成了这篇（还很不成熟的）文章。

假设赌徒和庄家赌博，这是一个公平的赌局，双方每把输赢的概率都是1/2 。庄家和赌徒的区别在于庄家手中有无限多的筹码。假设每次双方都押注一个筹码，赌徒只要还有筹码，就会继续赌下去，那么赌徒最终输光全部n个筹码的概率是多少呢？

https://zhuanlan.zhihu.com/p/77593762

在这篇文章中，求解思路是：

对于当前n个筹码的状态，设赌徒输光的概率为g(n)

押注后要么赢（p=1/2），此时赌徒拥有n+1个筹码by娱乐必赢，下一个状态赌徒输光的概率为g(n+1)

要么输（q=1/2），此时赌徒拥有n-1个筹码，下一个状态赌徒输光的概率为g(n-1)

于是可以得到以下递推式

博彩游戏

$g(n)=\frac{1}{2}g(n-1)+\frac{1}{2}g(n+1) \\ \Rightarrow g(n+1) - g(n) = g(n) - g(n-1)$

通过构造等差数列，最后可以解得g(n)=1恒成立

也就是说，在公平的赌博游戏中，本金有限的赌徒是玩不过本金无限的庄家的，只要一直玩下去，不离开赌场，赌徒的钱一定会输光。

我们在第一节说到，在概率公平的前提下，本金有限的赌徒必然破产，那赌徒赌多少次才会破产呢？如何计算押注次数的数学期望呢？

假设赌徒每次押注一个筹码，记获胜的概率为p，获胜后押注的筹码仍属于赌徒本人，并从庄家手中得到一个筹码（这句话有点啰嗦）；

记失败的概率为q，此时赌徒损失一个筹码。显然p+q=1。

按照第一章的思路，初始状态赌徒拥有k个筹码，记赌徒破产的押注次数的数学期望为 $d_{k}$ ，可以构造以下递推式：

$d_k = (1+d_{k+1})p + (1+d_{k-1})q,\ \ p+q=1 \$

递推式的意思是：每次押注，如果赌徒赢，则赌徒拥有了k+1个筹码，此时赌徒继续游戏直至破产，押注次数的数学期望是已经发生的1次加上未来的 $d_{k+1}$ 次；如果输了，则是已经发生的1次加上未来的 $d_{k-1}$ 次。两种情况对应的概率是p和q，且。

于是我们可以得到：

$d_k - pd_{k+1}-qd_{k-1}=1 \$

这是一个递推数列，它的解形式为，

$d_k=A\theta^{k}_{1}+B\theta^{k}_{2}+d_k^{part} \$

其中 $d_k^{part}$ 是特解，指数函数项为通解：

$d^{'}_k=A\theta^{k}_{1}+B\theta^{k}_{2}\\d^{'}_k - pd^{'}_{k+1}-qd^{'}_{k-1}=0\\d^{part}_k - pd^{part}_{k+1}-qd^{part}_{k-1}=1$

不少朋友会想到【这不就是微分方程的解的形式吗】，没错，确实是这样的，而且已经有大佬做了详细的讲解，我就不证了（溜了溜了）。

https://zhuanlan.zhihu.com/p/109529158

我们把 $\theta^{k}_{1}$ 和 $\theta^{k}_{2}$ 代入，正好是一元二次方程的形式：

$\theta^{k}-p \theta^{k+1}-q \theta^{k-1}=0 \\ \Rightarrow \theta^{k-1}(\theta-p\theta^{2}-q)=0$

相当于求解 $x^{2}-\frac{x}{p}+\frac{q}{p}=0$ ，得到 $x_1=1,x_2=\frac{q}{p}$ ，也就是有： $d_k^{'}=A+B(\frac{q}{p})^{k}$

对于 $d_k^{part}$ ，它的表达式显然（23333）为 $d_k^{part}=bk$ ，代入可得：

$bk-pb(k+1)-qb(k-1）=1 \\\Rightarrow bk-pk-pb-qbk+qb=1\\(q-p)b=1$

如果，则该方程无解，的表达式后面我们再想办法

如果 $p\ne q$ ，可得 $d_k^{part}=bk=\frac{k}{q-p}$ ，即 $d_k=A+B(\frac{q}{p})^{k}+\frac{k}{q-p}$

▍2.1 非公平赌博情况下（ $p\ne q$ ）的求解方法

显然当筹码数k=0时，游戏结束，，但k等于其他正整数时候，我们是不知道等于多少的，也就是说无法找到第二个关于A和B的方程，更加不可能找到的精确表达式了。

通过查找资料发现，教材上的例题直接给刚刚的赌徒破产问题增加了一个终止条件：

当赌徒赢得个筹码（）时候，赌徒见好就收，跑路不玩了！

这个时候就有两个关于A、B的方程，解这个二元一次方程组，就可以得到解析解！

$d_0=A+B=0\\ d_N=A+B(\frac{q}{p})^{N}+\frac{N}{q-p}=0 \\d_k=\frac{k}{q-p}-\frac{N}{q-p} \frac{(1-(q/p)^k)}{(1-(q/p)^N)}，p\ne q$

▍2.2 公平赌博情况下（ ）的求解方法

我们重新回到刚才的情况，代入下式，对于我们有： $d_k - pd_{k+1}-qd_{k-1}=1 \\\Rightarrow d_k=\frac{1}{2}d_{k+1}+\frac{1}{2}d_{k-1}+1 \\ \Rightarrow d_{k+1} - d_k = d_k - d_{k-1} -2$

令 $S_k = d_k - d_{k-1} \ (k\geq1)$ ，可得： $S_k-S_{k-1}=-2$ ，也就是说是等差数列，设 $S_k =-2k+b \ (k\geq1)$ 于是有：

$d_k-d_{k-1}=-2k+b\\ \ d_{k-1}-d_{k-2}=-2(k-1)+b\\...\\d_1-d_0=-2+b$

将这k个等式左右两边求和，等差数列等于（首项+末项）*项数除以2，可得：

$d_k-d_0=[(-2k+b)+(-2+b)]\times\frac{k}{2}=k(b-k-1) \$

而且因为赌徒在输光或赢得N块钱时候离场，所以有: ，代入上式：

$d_N-d_0=d_N=N(b-N-1)=0\\ \Rightarrow b=N+1$

所以，当，赌徒在输光或赢得个筹码后离场的押注次数的数学期望为。

经过前面的铺垫，我们回到刚才的问题：

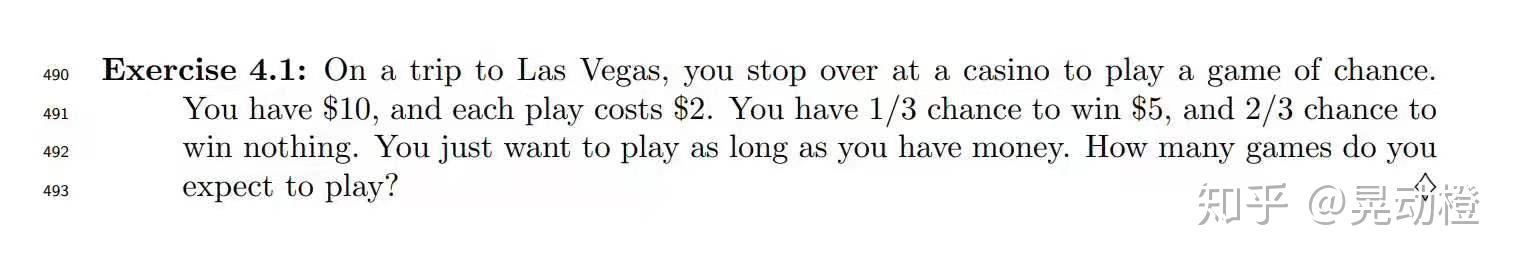
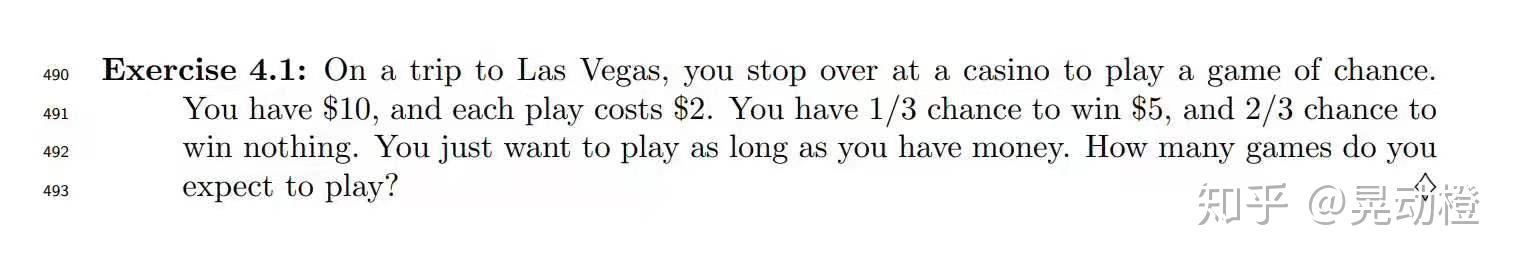
类比前面两节【要么赢，要么输】的递推式思路，如果赌徒获胜，他的收益是5-2=3美元，如果失利，他的收益是-2美元，设赌徒拥有k美元时，一直押注直至输光的游戏次数的数学期望为，则有：

$d_k=1+\frac{1}{3}d_{k+3}+\frac{2}{3}d_{k-2} \ (k\geq2) \$

它对应的特征方程是一元五次方程，也有类似于常微分方程的解的形式： $d_k=d_k^{part}+\sum_{i=1}^{5}{A_i\theta_i^{k}} \$

在上一节例题中，当随机游走只有一个吸收壁的时候，都不足以求出解析解，

现在我们面对的是一元五次方程，游戏终止的条件只有两个：或，此时赌徒钱不够玩了，但我们要求的系数有5个（实际上是4个，因为这个一元五次方程有两个复数解，假设他们对应系数是，为了把虚数i消掉，必定有），所以无法求出精确的。

但我们从直觉上简单分析:

赌徒押注一次，固定损失为2美元，而收益的数学期望为 $\frac{5}{3}$ 美元，

很显然，这个游戏是亏的，每次押注亏损的数学期望是 $\frac{1}{3}$ 美元，

赌徒初始状态有10美元，平均下来玩30次就破产了。更何况，不用等输光，当赌徒输至1美元时，他的钱已经不足以参与下一次押注，所以我们希望求解的 $d_{10}$ 必然小于30

这个数字具体应该是多少呢？

通过前面的铺垫我们知道因为方程数大于未知数的数量，无法得到解析解、

但毕竟是概率题，借助计算机的话还是有办法的

摆在我们面前有两个选择：

1、蒙特卡洛模拟，秒天秒地秒空气，秒掉所有概率题

2、列出所有押注结果，乘以对应的概率用计算机暴力求和

笔者采用的是第二种

——–暴力求解分割线——–

已知赌徒拥有10美元，每次押注需要花费2美元，假设赌徒押注n次后破产

我们首先考察n的取值范围：

1、显然n=5是合法的，只要连续输5次就破产了。

2、但是n=6是不合法的，因为：

1）假设赌徒前面五次押注一次没赢过，那他在赌到第五次就离场了；

2）假设赌徒前五次押注刚好赢过一次，押注第六次前赌徒正好拥有10-5*2+5=5美元，无论如何都可以再玩两次，输剩1美元再离场，所以n不可能等于6。

通过以上分析，我们设赌徒赢X次，输Y次后离场（此时赌徒拥有0美元或1美元，已无法再参与游戏），总押注次数为X+Y=N：

$\begin{equation} \left\{ \begin{array}{lr} X+Y=N\\10+5X-2N=0 \end{array} \right. \end{equation}$ 或 $\begin{equation} \left\{ \begin{array}{lr} X+Y=N\\10+5X-2N=1 \end{array} \right. \end{equation}$

因为X、Y、N必须为非负整数，可得：

$\begin{equation} \left\{ \begin{array}{lr} X=2k-2\\Y=3k+2\\N=5k \end{array} \right. \end{equation} \ \ (k\geq1)$ 或者 $\begin{equation} \left\{ \begin{array}{lr} X=2k-1\\Y=3k+3\\N=5k+2 \end{array} \right. \end{equation} \ \ (k\geq1)$

所以合法的N的取值序列为或

设这样的取值序列为数组Tn，按升序排列：

T[0]=5，T[1]=7，T[2]=12，T[3]=15….

显然，对于每一个合法的N的取值序列，对应获胜次数X也可以用数组Xn来存放（Y同理）：

X[0]=0，X[1]=1，X[2]=2，X[3]=3….

至此我们已经找到了所有合法的游戏终止时玩家押注次数Tn的表达式，以及获胜次数X，失败次数Y的表达式。接下来我们开始计算玩家押注结果的排列数：

1、考虑T[0]=5，X[0]=0的情况，简单标记胜利为W，失败为L，显然只有一种押注结果：

【LLLLL】，对应概率为 $(\frac{2}{3})^{5}$

2、考虑T[1]=7，X[1]=0的情况，此时押注结果有7种：

【WLLLLLL】，【LWLLLLL】、【LLWLLLL】、【LLLWLLL】、【LLLLWLL】、【LLLLLWL】、【LLLLLLW】，每一种情况对应概率为 $(\frac{2}{3})^{6}(\frac{1}{3})^{1}$ ；

细心的朋友会发现【最后两种情况根本不合法啊必赢亚洲网址，赌徒前面五次都输了，早就就拜拜了】所以此时真正合法的押注结果排列只有5种

3、考虑T[2]=10，X[2]=2的情况，此时押注结果有 $C_{10}^{2}=45$ 种，，每一种情况对应概率为 $(\frac{2}{3})^{8}(\frac{1}{3})^{2}$ ，同样的，我们必须把所有不合法押注结果减掉，具体来说，就是对于押注10次的所有可能的45种排列：

1）把以【LLLLL】开头的押注结果去除掉，一共有种（前5次全输，剩下的5次押注，赢2次输3次）；

2）把以【WLLLLLL】，【LWLLLLL】、【LLWLLLL】、【LLLWLLL】、【LLLLWLL】开头的押注结果去除掉，一共有 $5\times C_3^1=15$ 种（前面7次1胜6负（对应5种排列情况），剩下的3次押注，赢1次输2次）；

所以T[2]=10，X[2]=2时，合法的押注结果排列只有 $C_{10}^2-C_5^2\times1-C_3^1\times5=20$ 种。

我们按照电脑数组的下标，记T[i]、X[i]对应的合法押注结果排列数为dp[i]（懒得想名字，就用动态规划来命名了），用代码重写 $C_{10}^2-C_5^2\times1-C_3^1\times5=20$ 这个式子：

from scipy.special import comb #comb是组合数函数
dp[2]=comb(T[2],X[2])
      -comb(T[2]-T[0]必赢亚洲,X[2]-X[0])*dp[0] #剩下的5次押注，赢2次
      -comb(T[2]-T[1],X[2]-X[1])*dp[1] #剩下的3次押注，赢1次

i=3同理，可得dp[3]=220-35-50-40=95：

dp[3]=comb(T[3],X[3])
      -comb(T[3]-T[0],X[3]-X[0])*dp[0] #剩下的7次押注，赢3次
      -comb(T[3]-T[1],X[3]-X[1])*dp[1] #剩下的5次押注，赢2次
      -comb(T[3]-T[2],X[3]-X[2])*dp[2] #剩下的2次押注，赢1次

我们只要写出上式的for循环，就可以求出所有T[i]、X[i]对应的排列数dp[i]，最后乘以发生的概率和游戏次数： $\sum_{i=0}^{ \infty}{(\frac{2}{3})^{Y[i]}(\frac{1}{3})^{X[i]}}\times dp[i]\times T[i] \$

我的Python精度只能求和到第400项，i=400，T=1002，X=399，Y=602，得到最后的期望的近似值是28.409727793196275，比30小一点，应该没错了，完结撒花！

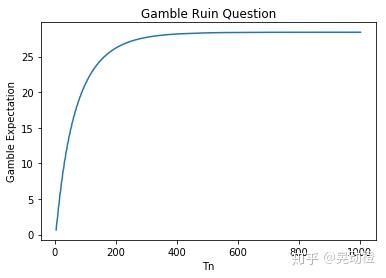
最后附上代码：

# -*- coding: utf-8 -*-
"""
Created on Sat Dec 19 16:33:08 2020
@author: HDC
"""

from scipy.special import comb
import numpy as np

step = 400
dp = np.zeros(step)
dp[0]=1
t_series = np.zeros(step)


def func_t(n):
    if (n & 1) == 0:  #print("{0} 是偶数".format(n))
        k = n/2
        t=5*k+2
        x=2*k-1
        y=3*k+3    
    else:
        #print("{0} 是奇数".format(n))
        k = (n+1)/2
        t=5*k
        x=2*k-2
        y=3*k+2
    t_series[n-1] = t    
    tup = (t,x,y)
    return tup

def func_s(n, dp):
    if(n==1):
        return 1
    tup_n = func_t(n)
    tn = tup_n[0]
    xn = tup_n[1]
    yn = tup_n[2]
    comb_series = np.zeros(n)
    for i in range(1,n):
        tup_i = func_t(i)
        c_all = tn - tup_i[0]    
        c_x = xn - tup_i[1]
        comb_series[i-1] = comb(c_all,c_x)
    
    dot_multi_series = np.zeros(n)
    for i in range(0,n):
        dot_multi_series[i] = comb_series[i] * dp[i]
    sn = comb(tn,xn) - sum(dot_multi_series)
    dp[n-1] = sn
    return sn

posibility = np.zeros(step)博狗娱乐boodog
for i in range(0,step):
    tup = func_t(i+1)
    x = tup[1]
    y = tup[2]
    posibility[i] = np.power(1/3,x) * np.power(2/3,y)   
    
for i in range(1,step+1):
    func_s(i, dp)
    
result = np.zeros(step)
tmp = 0
for i in range(0,step):
    tmp = tmp + posibility[i] * dp[i] * t_series[i]
    result[i] = tmp
print (result[-1])

from matplotlib import pyplot as plt 
plt.title("Gamble Ruin Question") 
plt.xlabel("Tn") 
plt.ylabel("Gamble Expectation") 
plt.plot(t_series,result) 

plt 博彩游戏.show()

博彩游戏

博彩游戏：赌徒破产问题中押注次数的数学期望求解，by娱乐必赢

相关文章 :

2025 年 9 月
一	二	三	四	五	六	日
1	2	3	4	5	6	7
8	9	10	11	12	13	14
15	16	17	18	19	20	21
22	23	24	25	26	27	28
29	30